
Mapping the Capacity–Conductance Boundary in VRLA Lead-Acid Batteries
Mr. Kasiean Sukemoke
Founder & MD
PDF Content
All of Our Knowledges

Lead-Acid Battery Fundamentals: How They Work, Types, and Lifespan
A complete guide to the fundamentals of lead-acid batteries. Learn about their working principles, structure, classifications (Flooded, VRLA, AGM, Gel), and the key factors like temperature and discharge that affect capacity and lifespan.

Battery Showdown: Lithium-ion vs. Advanced Lead Carbon VRLA for Stationary Applications
As the world increasingly relies on renewable energy and robust power grids, the demand for effective stationary energy storage solutions has surged. Two leading technologies dominate this space: Lithium-ion (LiB) and Advanced Lead Carbon VRLA (Valve-Regulated Lead-Acid) batteries. While Lithium-ion is known for its high performance and energy density, Advanced Lead Carbon offers a reliable and cost-effective alternative. This article provides a comprehensive comparison of these two battery types across technical specifications, safety, economics, and application suitability to help determine the best choice for various stationary uses.

Dynasty VRLA Battery System: Maintenance and Troubleshooting Guide
Valve-Regulated Lead-Acid (VRLA) batteries are widely used in backup power systems due to their sealed design and low maintenance requirements. However, to ensure reliable performance and long service life, regular inspection and systematic maintenance are essential. This guide summarizes the **periodic maintenance steps**, **troubleshooting methods**, and **best practices** for Dynasty VRLA battery systems.

Battery System Installation & Start-Up: A Clear, Practical Guide
This guide distills the uploaded “Battery System Installation and Start-Up Instructions” into a concise, field-ready article. It focuses on safety, preparation, installation sequencing, initial charging (“freshening charge”), and post-install checks for VRLA (valve-regulated lead–acid) battery systems.*

Why Lead-Acid Batteries Fail — Practical Causes, Diagnostics, and Prevention
Lead-acid batteries (flooded and VRLA/AGM/Gel) usually fail for predictable, preventable reasons. This article organizes the common failure modes, explains the electrochemistry in plain language, and outlines field diagnostics and maintenance practices to extend service life.

Battery Health Testing with Impedance & Conductance: A Clear, Practical Guide
Impedance and conductance tests provide a fast, non-destructive way to assess battery health—especially for lead-acid and VRLA cells—without doing a full discharge test. This article explains what these tests measure, why baseline values matter more than one-off readings, and how to build a simple trending program that reliably flags aging cells before they fail.

Thermal Runaway in Lead-Acid Batteries: Causes, Risks, and Practical Prevention
Thermal runaway is a dangerous feedback phenomenon in battery systems where rising temperature drives higher charging current, which in turn generates more heat—potentially leading to swelling, venting, or even fire.* This article explains the mechanism in plain language and distills field-ready practices to prevent it.
Capacity Testing of VRLA Batteries: A Clear, Practical Guide
Capacity testing verifies whether a valve-regulated lead–acid (VRLA) battery bank can still deliver the current or power promised by its manufacturer over a specified time at a defined end-of-discharge voltage and temperature. This guide turns the technical procedure into a step-by-step checklist you can use in the field, with simple math to calculate the **Rated Capacity (%)** and account for temperature

Mapping the Capacity–Conductance Boundary in VRLA Lead-Acid Batteries
This article distills a technical study into a practical, plain-English guide on how **electrolyte conductance** and **deliverable capacity** relate inside **VRLA (valve-regulated lead-acid)** batteries. By modeling the **electrolyte** (acid + water) and the **plates** (active materials) separately—and then combining their constraints—we obtain **upper and lower bounds** that define where a battery’s **normalized conductance** \(G_d/G_n\) and **normalized capacity** \(Ah_d/Ah_n\) can realistically sit. The result helps field engineers interpret conductance readings, separate **undercharge/sulfation** from **electrolyte dry-out**, and decide when capacity testing or replacement is justified.

Lithium-Ion vs. Premium Pure-Lead VRLA Batteries for UPS Applications
When it comes to Uninterruptible Power Supply (UPS) systems, choosing the right battery technology is critical. Two of the most common contenders are **Lithium-Ion (Li-ion, specifically LFP)** and **Premium Pure-Lead Acid VRLA (TPPL)**. This article compares their **safety** and **performance** attributes against traditional VRLA batteries to help businesses and engineers make informed decisions.

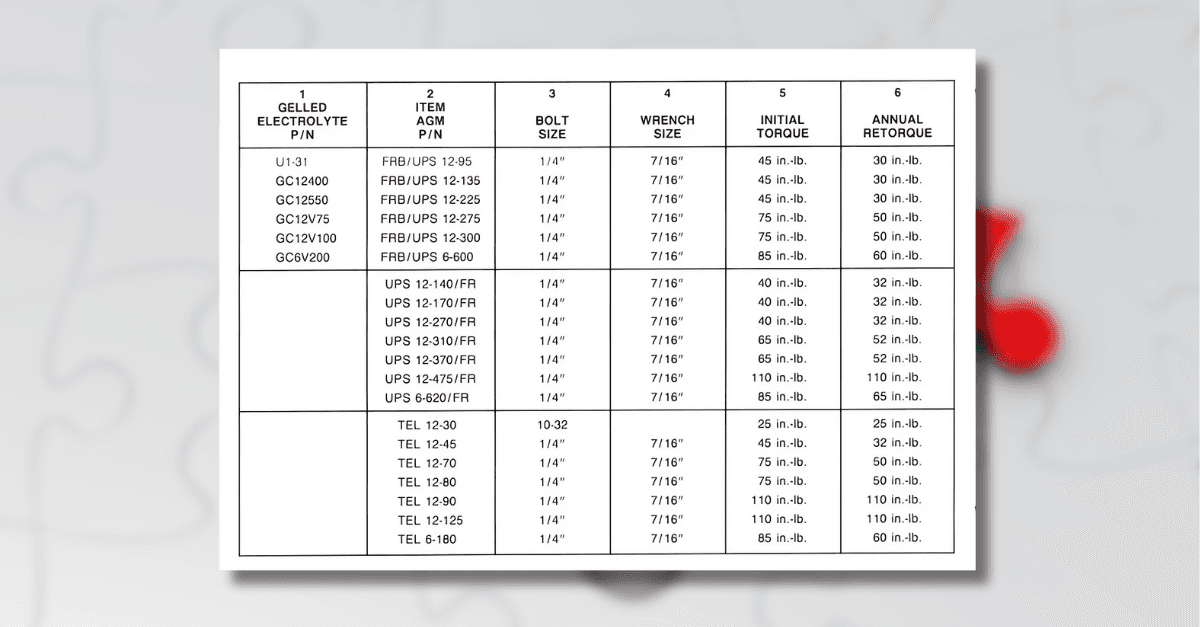
Choosing and Using VRLA Batteries (AGM vs. Gel): A Practical Guide
Valve Regulated Lead-Acid (VRLA) batteries are widely used in critical power systems because they’re sealed, low-maintenance, and safe when operated correctly. This guide explains how VRLA batteries work, compares Absorbent Glass Mat (AGM) and Gel technologies, and gives clear, field-ready advice for selecting the right type and operating it for long life.
Ready to Upgrade Your Power Infrastructure?
Connect with PEC Technology Today!
- Call: 02 907 8521
- Email: sales@pectecth.co.th
- Visit us at: 181‑183 Sukontasawat Rd., Ladprao, Bangkok
Secure reliable power. Minimize downtime. Future‑proof your systems.


